Om Kageformen, eller selve Kagen,

Er Hovedsagen

I denne Verden, gaae vi her forbi;

Jeg bringer – (ja, jeg kommer til det samme!)

Jeg bringer nemlig her en lille Ramme

Til hvad jeg skrev og kaldte Poesie,

(Tidt kun en Skizze, tidt et Malerie),

Dog, mueligviis faaer Rammen mest Værdie,

Thi der er Form og Politur heri,

Og Form – ja, »Formens evige Magie«,

Kan sagtens stikke Hjertets Poesie.

Han, som til Dato vragede hvert Stykke,

Jeg bragte frem, (fordi det eier Skygge),

Maaskee hos ham min Ramme her gjør Lykke,

Thi jeg skal trænge den i Formen ind;

Og neppe støder det min Mesters Sind

Hvor simpelt Stoffet er, hvoraf vi bygge;

Jeg vil den seige Prosa-Lyng oprykke,

Og kortsagt – lave Suppe paa en Pind;

Hvad der er mest mod Poesien bister,

Geometriens yndede ▶Magister

Matheseos◀, det gode gamle Skind,

I skjønne Former jeg paa Bladet rister.

Pas paa Enhver!

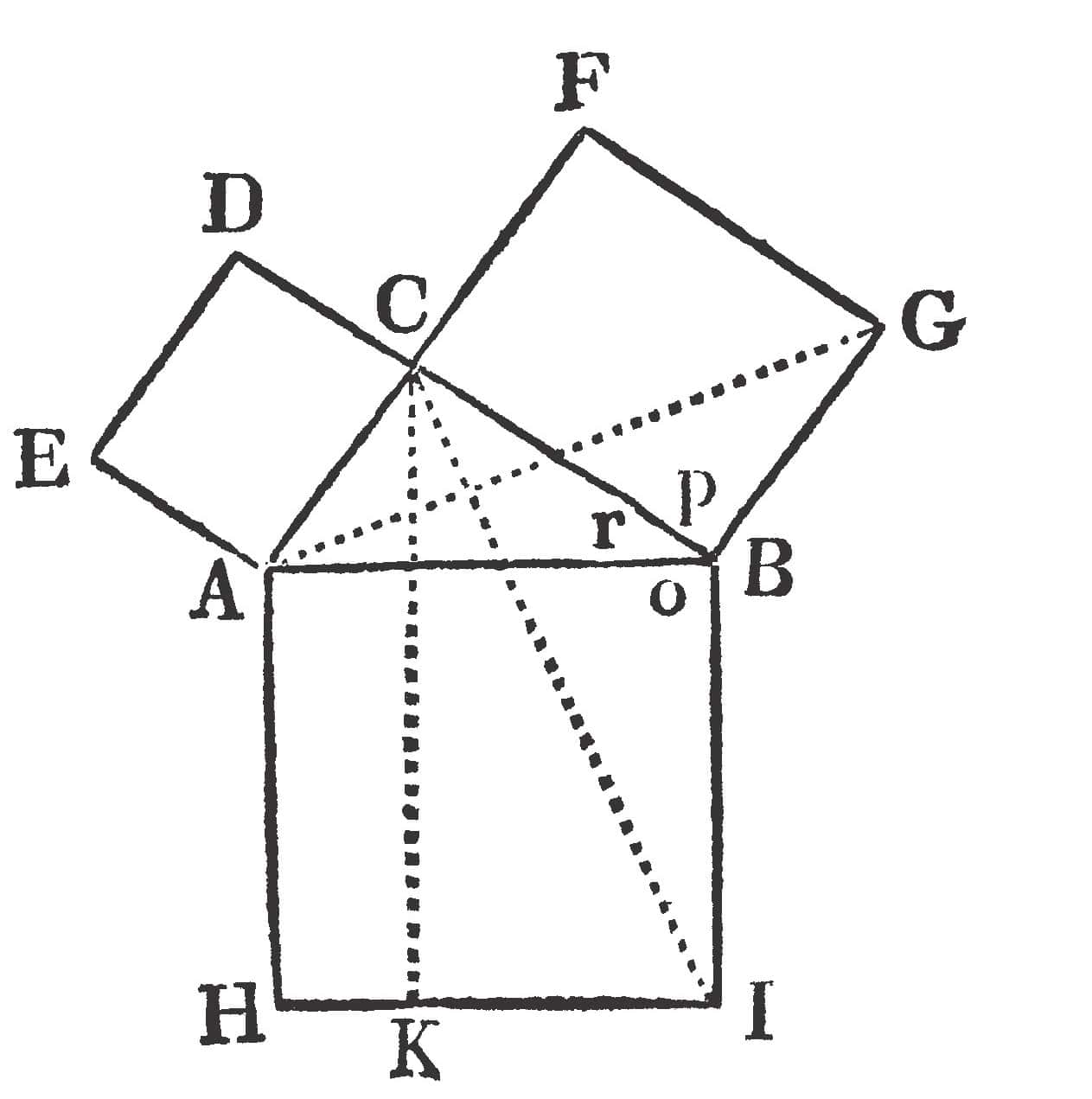
Trianglen A B C er givet her,

Retvinklet og paa Siderne Qvadrater;

▶Det, som ved disse skal bevises her,

Er at Qvadraterne paa hver Catheder

A C, B C (jeg nævner disse Steder)

Er’ just saa store her som den Krabat,

Hypothenusen kalder sin Qvadrat◀.

Nu gaae vi da til vore Præparater.

Her allerførst, saa Tingene behage,

Vi drage

En lodret Linie – det nok skal lide! –

Ned til den større Side,

Og saa forlænges den endnu til K,

Da vil man finde, uden mindste Mangler,

A B Qvadraten for vort Øie staae

Deelt som (A K, B K) i to Rectangler.

(Thi tvende rette Linier, man veed,

Har just det generelle,

Naar paa en tredie de staae lodret’ ned,

Saa veed man ogsaa, de er’ paralelle).

Nu drages een fra A til G, fra C til I,

Og al Præparationen er forbi.

Ei sandt, o Mester! – true dog ei med Riset!

Nu gaae vi til Beviset!

– Vi har de to Triangler A B G

Og C B I, hos dem er Vinklen p

Liig Vinklen o, men o er liig en ret,

(Thi rette Vinkler er der i Qvadrater),

Og Vinklen r liig Vinklen r. Ei sandt?

(Thi sund Fornuft kan sige,

Hver Størrelse jo med sig selv er lige)

Heraf man fandt,

At p plus r er liig med o plus r.

(Betragt dem nær,

Her i Figuren staae de smaae Krabater,)

Naar lige nu til begge bliver streget,

Saa bliver altid Summen lige meget.

– Fat Mod, nu er Beviset snart forbi,

Det alt mod Enden lider!

See Vinklen A B G liig C B I,

A B er liig B I, B G er liig B C

(I en Qvadrat er’ ligestore Sider);

Derfor, saa sandt som tre gjør’ altid tre,

(To Sider og en Vinkel vil os lette)

Trianglen A B G vi her tør sætte

Liig C B I, (og det er intet Træf!)

Nu A B G er liig en halv B F,

(Lidt videre vi maae)

Og C B I er liig en halv B K.

(De tvende halve passe nok saa søde,

Thi Ligestort for Ligestort kan møde)

Eens er Divisor, eens er Dividenten;

Eens bliver altsaa ogsaa Qvotienten,

Og nu paa samme Vei vi siden faae,

A D er liig A K.

Nu veed man Maaden,

Snart som Pythagoras man løser Gaaden.

– Men Gud skee Lov, at det er nu forbi!

Thi, slige Vers er’ ikke Narrerie,

De løbe vel, som der var Intet i –

– Dog her var jo Fornuft og Form-Magie,

(Det sidste vil jeg haabe;

Men denne Form er i det mindste fri

For hvad der dæmper slemt hver Melodie,

En Mudderdraabe).

Som sagt Fornuft og Formen, den er i,

Gjør jo at Rammen her er – Poesie.

Der seer man »Formens evige Magie!«